
Review studies are vital for advancing knowledge in many scientific fields, including mathematics education, amid burgeoning publications. Based on an extensive consideration of existing review typologies, we conducted a meta-review and bibliometric analysis to provide a comprehensive overview of and deeper insights into review studies within mathematics education. After searching Web of Science, we identified 259 review studies, revealing a significant increase in such studies over the last five years. Systematic reviews were the most prevalent type, followed by meta-analyses, generic literature reviews, and scoping reviews. On average, the review studies had a sample size of 99, with the Preferred Reporting Items for Systematic Reviews and Meta-Analysis (PRISMA) guidelines commonly employed. Despite certain studies offering nuanced distinctions among review types, ambiguity persisted. Only about a quarter of the studies explicitly reported employing specific theoretical frameworks (particularly, technology, knowledge, and competence models). Co-authored publications were most common within American institutions and the leading countries are the United States, Germany, China, Australia, and England in publishing most review studies. Educational review journals, educational psychology journals, special education journals, educational technology journals, and mathematics education journals provided platforms for review studies, and prominent research topics included digital technologies, teacher education, mathematics achievement, and learning disabilities. In this study, we synthesised a range of reviews to facilitate readers’ comprehension of conceptual congruities and disparities across various review types, as well as to track current research trends. The results suggest that there is a need for discipline-specific standards and guidelines for different types of mathematics education reviews, which may lead to more high-quality review studies to enhance progress in mathematics education.

Avoid common mistakes on your manuscript.
Comprehensive literature reviews serve as foundational pillars for advancing scholarly discourse, offering critical insights into existing research and shaping future inquiries across disciplines. In the realm of academic writing, spanning from journal articles to dissertations, literature reviews are highly regarded for their capacity to synthesize knowledge, identify gaps, and provide a cohesive framework for understanding complex topics (Boote & Beile, 2005). Moreover, reviews play a significant role in academia by setting new research agendas and informing decision-making processes in practice, policy, and society (Kunisch et al., 2023).
As empirical and theoretical research burgeons in diverse fields, the need for literature review studies has become even more pronounced, facilitating a deeper understanding of specific research areas or themes (Hart, 2018; Nane et al., 2023). Additional factors contributing to the popularity of review studies in recent years include the rise of specialized review journals (Kunisch et al., 2023), challenges associated with conducting various types of empirical studies during the prolonged COVID-19 crisis (Cevikbas & Kaiser, 2023), and a competitive research climate wherein factors such as impact factors and citations hold significant weight (Ketcham & Crawford, 2007). Review studies are particularly attractive as they often garner a substantial number of citations, thereby enhancing researchers’ visibility and scholarly impact (Grant & Booth, 2009; Taherdoost, 2023).
The importance of review studies has been duly acknowledged in mathematics education, as evidenced by the inclusion of review papers in thematically oriented special issues of journals such as ZDM– Mathematics Education (Kaiser & Schukajlow, 2024), which has been originally founded as review journal. Several upcoming or already published special issues of ZDM– Mathematics Education, which emphasise ‘reviews on important themes in mathematics education’, highlight the importance of review studies as valuable contributions to the field.
The proliferation of literature reviews has increased interest in developing typologies to categorise them and understand different literature review approaches (Grant & Booth, 2009; Paré et al., 2015; Schryen & Sperling, 2023). Despite its significance, there remains a notable lack of research aimed at comprehensively understanding review studies within the field of mathematics education from a meta-perspective. In response to this gap, we conducted a systematic meta-review with the aim of providing an overview of different types of review studies in mathematics education over the past few decades and consolidating insights from multiple high-level review studies (Becker & Oxman, 2008; Schryen & Sperling, 2023). Meta-reviews offer concise yet comprehensive synopses and curated lists of pertinent reviews, adeptly addressing the perennial challenge of balancing thorough coverage with focused specificity (Grant & Booth, 2009).
In addition, we applied bibliometric analysis as a valuable tool for identifying research trends, progress, reliable sources, and future directions within the field. The bibliometric analysis aids in identifying hot research topics and trends (Song et al., 2019), assessing progress, identifying reliable sources, recognising major contributors, and predicting future research success (Geng et al., 2017). Furthermore, it helps researchers to pinpoint potential topics, suitable institutions for cooperation, and potential scholars for scientific collaboration (Martínez et al., 2015). By combining a meta-review and bibliometric analysis, we aim to offer a comprehensive overview of and deeper insights into state-of-the-art review studies within mathematics education.
Specifically, we seek to understand how the distribution and development of literature review studies in mathematics education have evolved over the years, examining factors such as publication years, publishers, review types, sample sizes, and the use of theoretical or conceptual frameworks. Additionally, we aim to assess adherence to review study guidelines and protocols, providing insights into the rigor and quality of research methodologies employed, particularly in light of the lack of clear guidance on producing rigorous and impactful literature reviews (Kunisch et al., 2023).
Furthermore, we endeavour to identify authors who have made contribution to the field of mathematics education through review studies, as well as those whose work is most frequently cited. We also identify co-authorship network analysis as understanding research networks allows researchers to identify potential collaborators and build partnerships with other scholars in various countries. Collaborative research endeavours can lead to enhanced research outcomes, broader dissemination of findings, and increased opportunities for funding and professional development. It can also highlight interdisciplinary connections and collaborations within and across fields, leading to innovative approaches and solutions to complex research questions (RQs) that transcend disciplinary boundaries.
Moreover, we analysed the distribution of common keywords across review studies, identifying focal subjects and thematic areas prevalent in mathematics education research. This analysis can provide valuable insights into key topics and trends shaping the field, guiding future research directions and priorities.
Lastly, we identified the most cited review papers in mathematics education and the journals in which they have been published, recognizing seminal works and influential publications that have contributed to the advancement of the field.
Overall, in light of the preceding discourse, we addressed the following RQs to uncover the characteristics of review studies, identify research trends, and delineate future research directions in mathematics education:
In this chapter, we provide a thorough analysis of different typologies for review studies, as we seek to elucidate the primary characteristics of various review studies conducted within mathematics education (Sect. 2.1). This effort led to the identification of 28 review types presented in Table 1, which were used in the current study’s literature search processes to access existing review studies and the analysis of identified studies in the field of mathematics education. Furthermore, we discuss the advancement of guidelines and protocols, highlighting their role in shaping the conduct of review studies (Sect. 2.2). Finally, we conclude the chapter by underscoring the importance and potential impact of meta-reviews and bibliometric analyses in the context of mathematics education (Sect. 2.3).
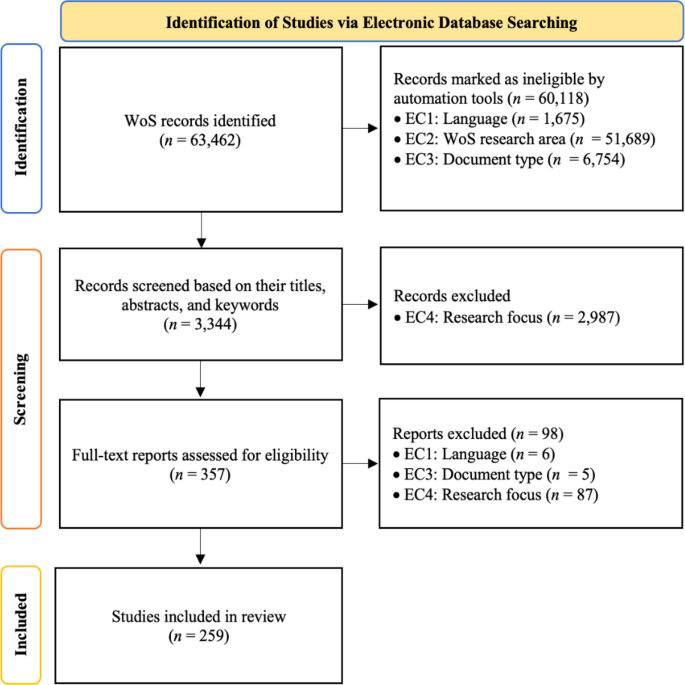
After incorporating 259 studies into this meta-review and bibliometric analysis, we compiled the identified records into a marked list on WoS. Subsequently, we exported the records into Excel, EndNote, and plain text file formats for analysis. The analysis consisted of content analysis and bibliometric analysis (see Fig. 2, adapted from Wei et al., 2023).
For the content analysis, we meticulously organised the records using EndNote reference management software and Excel worksheets. We scrutinised the full-text versions of all included articles, coding them based on (1) publication year, (2) publisher, (3) review type, (4) number of included studies (sample size), (5) guidelines and protocols for the article selection process, and (6) the theoretical and conceptual framework of the studies.
Our coding manual, informed by prior studies (Cevikbas et al., 2022, 2024), guided this process (see appendix for a sample of the coding manual). After completing the content analysis coding procedure, 20% of the papers (n = 52) were double-coded based on the initial coding protocol. The intercoder reliability, gauged at 0.92, signifies the presence of a coding system that exhibits satisfactory reliability (Creswell, 2013). Any discrepancies were addressed through discussions among the coders until consensus was reached.
For the bibliometric analysis, we employed VOSviewer software (version 1.6.20), which is widely recognised and extensively used in various fields, including the educational sciences (van Eck & Waltman, 2010). Chigbu et al. (2023) pointed out that the WoS database plays a pivotal role in facilitating bibliometric analyses across various disciplines. These analyses help establish trends in the development and application of knowledge within specific subjects and disciplines.
In our study, the bibliometric network presented in the results chapter consists of nodes and edges, with nodes representing entities such as publications, journals, researchers, or keywords. Edges denote relationships between pairs of nodes, indicating not only the presence or absence of connections but also conveying the intensity or strength of relationships (van Eck & Waltman, 2010). For distance-based approaches, the positioning of nodes in a bibliometric network reflects their approximate relatedness based on proximity.
Utilising VOSviewer software, we conducted (1) co-authorship analysis (authors and countries) to elucidate collaboration patterns and contributions, (2) co-occurrence analysis (focusing Author Keywords) to scrutinise knowledge structures and the distribution and development of key research topics in mathematics education, and (3) citation analysis to delve deeper into research influences and citation networks, drawing insights from the documents and sources.
This multifaceted approach allowed us to gain a comprehensive understanding of the bibliometric landscape and unravel collaborative structures, thematic foci, and the influence of key works on mathematics education.
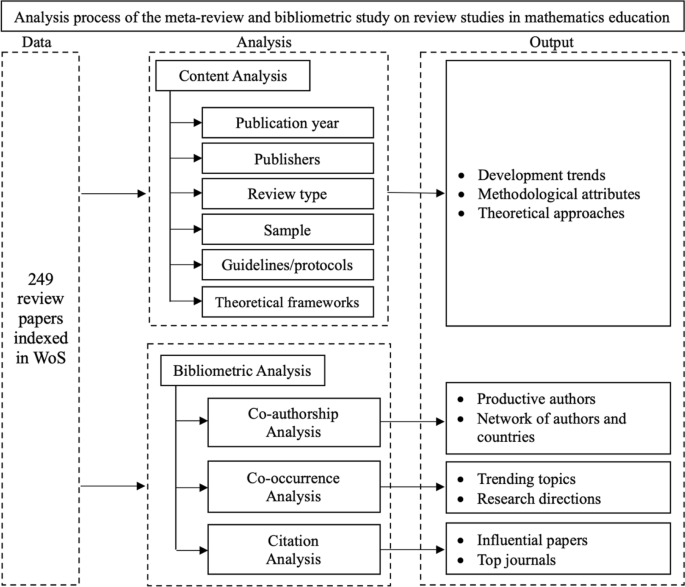
In this chapter, we present the key results of the meta-review and bibliometric analyses divided into two main categories: an overview of the review studies in mathematics education based on the content analysis, addressing RQ1, and the results of the bibliometric analysis, addressing RQ2–RQ5.
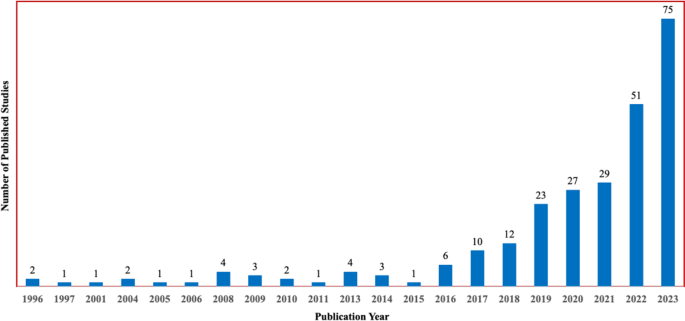
To discern the research trends and essential attributes of review studies in mathematics education, we conducted a content analysis within our meta-review to examine the 259 included review studies. Our analysis encompassed publication years, publishers, review types, guidelines, protocols used, sample sizes, and the theoretical and conceptual frameworks employed in these review studies. A general overview of the included studies is presented in Table 3.
The analysis showed that the Springer Group is the primary publisher of review articles in mathematics education, followed by Taylor & Francis, Elsevier, Sage, Frontiers, Wiley, MDPI, and the American Psychological Association (APA) (see Table 4). Other publishers published the remaining review articles (n = 43). This result may be attributed to the predominance of mathematics education journals published by Springer within the WoS database.
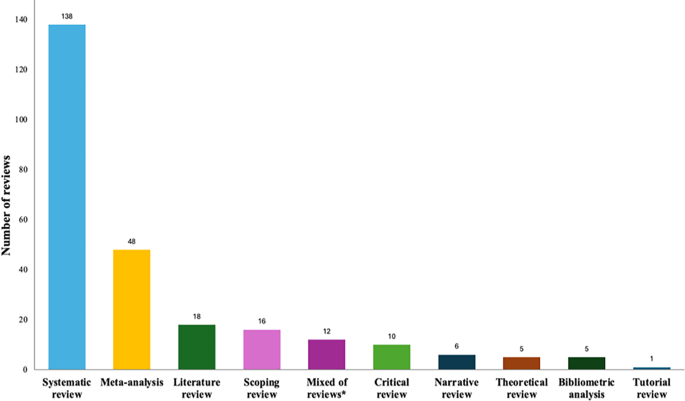
Our analysis did not yield further review types in mathematics education. Time-related analysis showed that recent studies were systematic reviews, meta-analyses, literature reviews, and scoping reviews, whereas early examples of review studies in mathematics education were primarily narrative or critical reviews or were not explicitly classified according to review type by their authors. Figure 4 shows that some researchers (n = 18) described their studies as literature reviews using Grant and Booth’s (2009) generic term, without providing further details about the type of review.
To comprehend the methodologies employed by researchers to conduct reviews and select eligible studies, we conducted an analysis of the guidelines and protocols the researchers used. The findings revealed that the PRISMA guidelines were the most frequently employed (n = 121), aligning with the distribution of review types—PRISMA guidelines are basically recommended for systematic reviews and meta-analyses (Page et al., 2021). For scoping reviews, the guidelines developed by Arksey and O’Malley (2005) were the most prevalent and were used in seven studies. In six instances, researchers applied various guidelines (e.g. PICO or SALSA guidelines) sourced from the literature. Almost half of the studies (n = 125) did not specify the use of guidelines for conducting literature searches and selecting eligible studies. Additionally, three studies aimed to provide protocols for conducting review studies. Furthermore, seven studies were preregistered as review studies, following the Open Science Framework (OSF) and/or the International Prospective Register of Systematic Reviews (PROSPERO) protocol.
A prevalent discourse among researchers in review studies revolved around determining the most suitable number of studies to include in reviews. Our results revealed that the sample sizes of the included studies (i.e. the number of primary studies) in the field of mathematics education ranged from 8 to 3,485. Unfortunately, this information was not reported in 19 review articles. In the remaining 240 review articles, the average was 99 included studies, with an overall total of 23,761. Most of the studies (n = 202) had sample sizes of less than 100, with an average of 34 (see Table 5). Although we harboured concerns that the review studies identified in this investigation might not have been aptly named and conceptualised by their authors, we deliberately refrained from addressing this issue because it fell outside the scope of our study. While including a substantial number of studies is common and potentially suitable for bibliometric analyses and meta-analyses, conducting a systematic review, scoping review, or narrative review that critically analyses exceptionally high volumes of studies may pose challenges. In this meta-review, for example, we observed that five articles included more than 1,000 studies in the review process. Two studies, enriched by bibliometric analysis, took this approach, while another study was identified by the authors as a scoping review with a sample size of 2,433. Additionally, two studies were labelled as systematic reviews with sample sizes of 1,968, and 3,485, respectively.
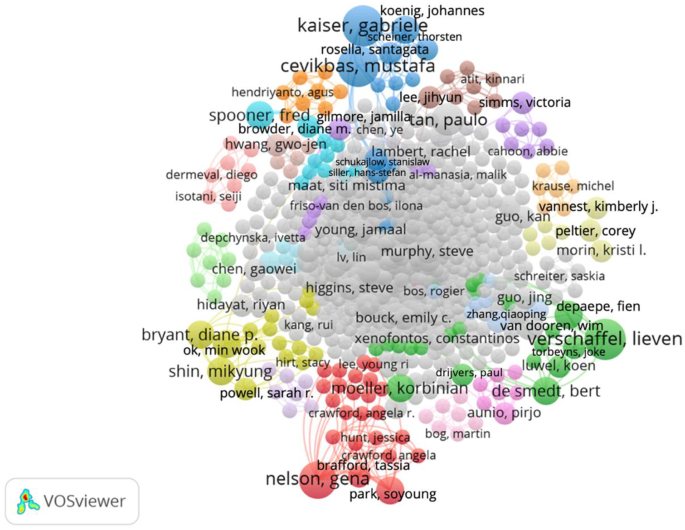
We conducted a co-authorship–country analysis, setting the minimum number of documents for a country as one, and identified 50 countries. This selection resulted in five clusters, each containing a minimum of five items (countries).
The most prominent cluster was the green cluster, encompassing eight countries from various global regions: the United States (US; TLS = 30), Germany (TLS = 23), Australia (TLS = 21), China (TLS = 11), South Korea (TLS = 6), Sweden (TLS = 4), New Zealand (TLS = 2), and Jordan (TLS = 1). The US dominated research collaborations both within this cluster and overall.
The red cluster included nine countries, predominantly Nordic and European countries: Norway (TLS = 13), Finland (TLS = 7), Belgium (TLS = 6), the Netherlands (TLS = 6), Lithuania (TLS = 1), Portugal (TLS = 1), Luxembourg (TLS = 1), Scotland (TLS = 1), and Israel (TLS = 1).
The yellow cluster contained seven countries: Canada (TLS = 7), Malaysia (TLS = 7), Denmark (TLS = 3), Libya (TLS = 2), Singapore (TLS = 2), Indonesia (TLS = 1), and the United Arab Emirates (TLS = 1).
The blue cluster primarily highlighted European collaborations and included seven countries: England (TLS = 22), Switzerland (TLS = 4), Italy (TLS = 3), France (TLS = 3), Greece (TLS = 1), Chile (TLS = 1), and Saudi Arabia (TLS = 1).
Lastly, the purple cluster represented a network of predominantly South and North American countries featuring, among others, Brazil (TLS = 6), Ireland (TLS = 5), Mexico (TLS = 4), Ecuador (TLS = 2), and Cuba (TLS = 2)(See Fig. 6).
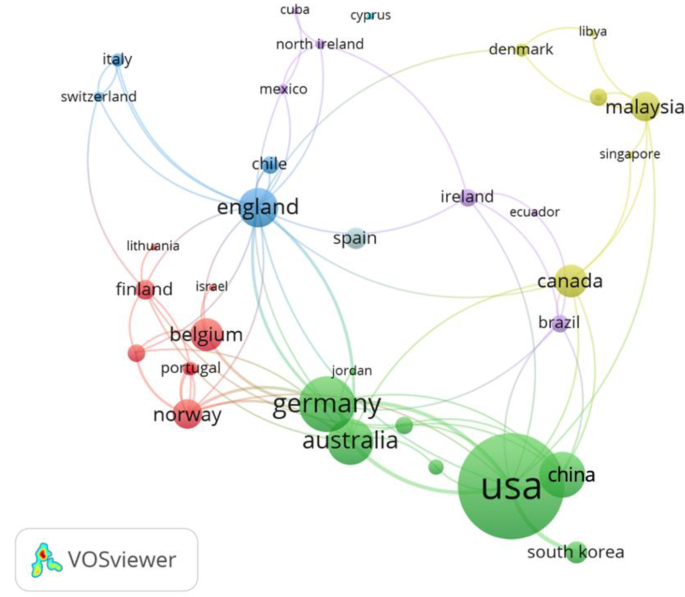
To explore the research hotspots within mathematics education, we ran a keyword co-occurrence analysis using Author Keywords.
The author keyword co-occurrence analysis indicated that our repository contained 691 keywords (see Fig. 7, left side), of which 23 met the minimum occurrence threshold of five occurrences (n = 5) (see Fig. 7, right side). In the figure, the size of a node corresponds to the frequency of a keyword co-selected in review studies in mathematics education. The distance between any two keywords reflects their relative strength and topic similarity. Nodes within the same colour cluster indicate similar topics among these publications.
The red cluster comprises 11 closely related items, including ‘mathematics, meta-analysis, mathematics achievement, intervention, scoping review, bibliometric analysis, review, technology, learning disabilities, children, and math anxiety’. The green cluster emerges as the second prominent cluster, featuring 8 interrelated items such as ‘mathematics education, systematic review, systematic literature review, literature review, teacher education, education, teaching, and flipped classroom’. Lastly, the blue cluster consists of 4 items, namely ‘math, science, early childhood, and identity’.
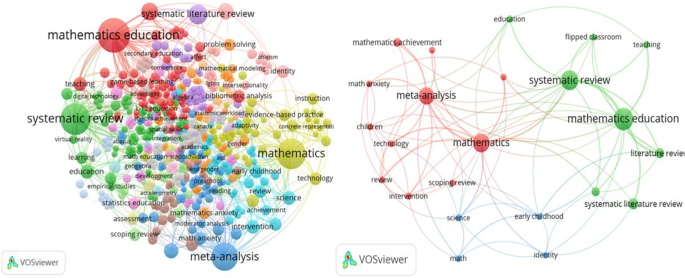
Notably, the most frequently cited author keyword was ‘mathematics education’ (n = 55), followed by ‘systematic review’ (n = 44), ‘mathematics’ (n = 41), ‘meta-analysis’ (n = 34), ‘systematic literature review’ (n = 14), ‘literature review’ (n = 11), ‘teacher education’ (n = 9), ‘mathematics achievement’ (n = 8), ‘intervention’ (n = 6), ‘education’ (n = 6), ‘teaching’ (n = 6), ‘science’ (n = 6), ‘scoping review’ (n = 5), ‘bibliometric analysis’ (n = 5), ‘review’ (n = 5), ‘math’ (n = 5), ‘technology’ (n = 5), ‘flipped classroom’ (n = 5), ‘early childhood’ (n = 5), ‘children’ (n = 5), ‘identity’ (n = 5), ‘learning disabilities’ (n = 5), and ‘math anxiety’ (n = 6).
The keywords chosen by the authors highlighted the focus areas of reviews in mathematics education, emphasising themes such as mathematics achievement, teacher education, interventions, technology, and technology-enhanced approaches (e.g. flipped classrooms), special education, and early childhood education. Furthermore, the author keywords reflected the prevalent review types in mathematics education, specifically systematic reviews and meta-analyses. Additionally, they highlighted the interdisciplinary nature of reviews in mathematics education, encompassing both mathematics education and science education.
Furthermore, we conducted distinct author keyword co-occurrence analyses for review studies published within the periods of 2019 to 2023 and those preceding 2019, aiming to discern temporal trends in author keywords, particularly in recent years. The analysis yielded 606 keywords for the 2019–2023 period and 144 keywords for the period before 2019 (see Table 8 for the most popular 15 author keywords). A noteworthy disparity in prevalent keywords was observed between the two temporal segments. While predominant keyword regarding the review types prior to 2019 was meta-analysis, followed by literature review and systematic review, over the past five years, additional keywords such as scoping review and bibliometric analysis emerged, signalling an augmentation in the diversity of review types and methodologies. The findings indicated a notable increase in the popularity of systematic reviews over the past five years.
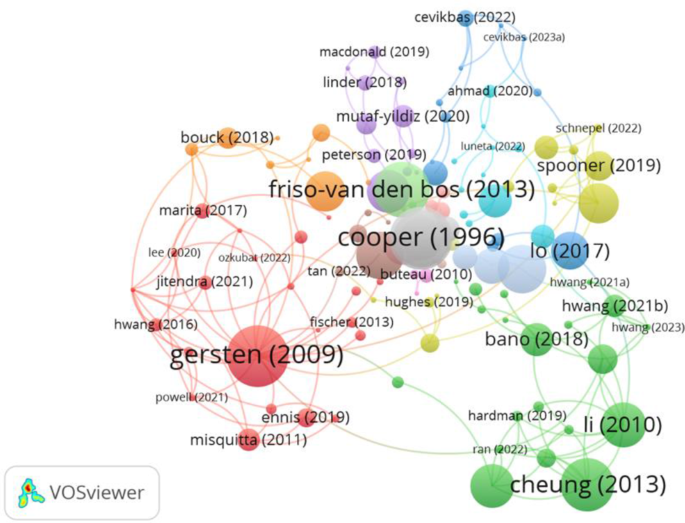
Our results showed that the largest number of citation links were for meta-analyses and systematic review studies. The most prominent review type among the most cited studies listed in Table 9 is meta-analysis (n = 6), followed by literature review (n = 2), systematic review (n = 1), and narrative review (n = 1). This result indicates the potential of meta-analysis studies in terms of citation performance. Most of these review studies were primarily published in high-ranking educational review journals (n = 6). Other review papers published in teacher education (n = 2), psychology (n = 1), and behavioural science and neuroscience journals (n = 1). These ten most cited review articles were all published in SSCI journals over a decade ago. Regarding research topics in the most cited papers, the dominant topics were mathematics achievement, content knowledge, working memory, learning disabilities, and educational technologies.
Specifically, we analysed the citation trends of the most cited 10 review papers over time and separately for the first five years after publication and the past five years (2019–2023). The results indicate a significant increase in the citations review studies have received in the last five years. We found that eight out of the ten most cited papers received more citations in the past five years (2019–2023) than in the first five years after their publication. The analysis revealed that the average annual citations for each paper ranged from 7 to 30. While the majority of these review studies (n = 8) received the least citations in the year of their publication, they received the most citations on average approximately 12 years after publication. This indicates that the peak citation period for review articles in mathematics education extends beyond the first decade following their publication.
The number of articles and the distribution of journals across various research fields were as follows: 25 educational sciences journals (43 papers), 20 psychology and educational psychology journals (41 papers), 15 special education journals (32 papers), 12 mathematics education journals (52 papers), 10 educational review journals (41 papers), 9 educational technology journals (28 papers), 3 mathematics journals (14 papers), and 9 other journals (8 articles).
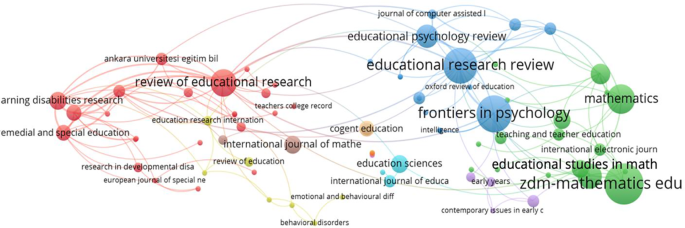
Our findings indicate that ZDM– Mathematics Education (n = 16) has, so far, published the most review studies focusing on mathematics education, which is not unexpected due to the origin of the journal as a review journal publishing only special issues, for which a review article is compulsory in each issue. This was followed by Frontiers in Psychology (n = 14), Educational Research Review (n = 13), and Mathematics (n = 10) (see Table 11 for the top 15 journals).
Table 11 Top journals publishing review studies in mathematics educationThe results highlighted that the most frequently cited papers were often published in specific educational review journals (e.g. Review of Educational Research, Educational Research Review, and Educational Psychology Review), psychology and educational psychology journals (e.g. Frontiers in Psychology, Educational Psychology Review, European Journal of Cognitive Psychology, and Psychological Bulletin), special education journals (e.g. Exceptional Children, Learning Disabilities Research & Practice, Learning Disability Quarterly, and Remedial and Special Education), educational technology journals (e.g. Computers & Education, Journal of Computer Assisted Learning, and Education and Information Technologies), and mathematics and mathematics education journals (e.g. ZDM– Mathematics Education, Educational Studies in Mathematics, and Mathematics).
Although the most visible mathematics education journals in citation network map were ZDM– Mathematics Education and Educational Studies in Mathematics (see Fig. 9), as mentioned earlier, twelve mathematics education journals provided platforms for review studies. These were ZDM– Mathematics Education (n = 16), Educational Studies in Mathematics (n = 5), International Journal of Science and Mathematics Education (n = 5), International Journal of Mathematical Education in Science and Technology (n = 5), International Electronic Journal of Mathematics Education (n = 3), Mathematics Education Research Journal (n = 3), International Journal for Technology in Mathematics Education (n = 3), International Journal of Education in Mathematics, Science and Technology (n = 3), Journal for Research in Mathematics Education (n = 2), Canadian Journal of Science, Mathematics and Technology Education (n = 1), Journal für Mathematik-Didaktik (n = 1), and Research in Mathematics Education (n = 1).
In this study, we conducted a meta-review of literature review studies in mathematics education, enriched by a comprehensive bibliometric analysis. This paper significantly contributes to scholarly discourse by unravelling nuanced research trends, the most common review methodologies, and prevalent theoretical approaches in review studies in mathematics education. Based on content and bibliometric analysis, it delves into the research foci, providing an understanding of the relevant academic landscape. Additionally, it illuminates intricate connections among researchers, countries, and journals, elucidating collaborative networks in mathematics education research.
The findings revealed a significant increase in the number of literature reviews in mathematics education, particularly in the past five years; 79% of the reviews we examined were published during this period. Multiple factors may have contributed to this surge, including researchers’ increased publication output during the pandemic (Cevikbas & Kaiser, 2023; Nane et al., 2023), challenges in collecting empirical data during the pandemic crisis (Uleanya & Yu, 2023), the relatively high citation rates associated with literature review studies, the growing prestige of educational review journals based on their increased impact factors (Miranda & Garcia-Carpintero, 2018), and the publication of review-oriented special issues in mathematics education journals.
Our findings revealed a prevalence of systematic reviews and meta-analyses; however, researchers also conducted diverse types of reviews, including scoping reviews, critical reviews, narrative reviews, theoretical reviews, and tutorial reviews. This methodological diversity is important as the advantages of one method can potentially overcome the disadvantages of another and combining different approaches can mitigate disadvantages (Taherdoost, 2023). Furthermore, our study revealed that rapid reviews, meta-reviews, umbrella reviews, mapping reviews, mixed-methods reviews, integrative reviews, interpretative reviews, iterative reviews, meta-syntheses, descriptive reviews, realist reviews, selective reviews, algorithmic reviews, and computational reviews indexed in WoS were not represented in mathematics education. The well-established PRISMA guidelines offer a defined framework for systematic reviews and meta-analyses to assist researchers in conducting reviews while adhering to quality and transparency criteria (Moher et al., 2009; Page et al., 2021). This adherence may have encouraged researchers to undertake such reviews, and future advancements in the development of specific guidelines and methodologies for each review type may further motivate researchers to conduct other types of reviews in mathematics education more frequently.
There were nuanced overlaps between the review types, leading to ambiguous distinctions. For instance, the structural similarity between systematic reviews and scoping reviews has led to misunderstandings. Munn et al. (2018) confirm inconsistency and confusion regarding the differentiation between scoping reviews and systematic reviews and offered guidelines for this decision-making process: a systematic review is preferable when addressing specific questions regarding the feasibility, appropriateness, significance, or efficacy of a specific treatment or practice. However, if the authors intend to demarcate the research field and explore its potential size and scope, a scoping review is more appropriate. Grant and Booth (2009) and Munn et al. (2018) clarified that a scoping review is preparation for a systematic literature review, not a deep study for a systematic literature review. The diverse taxonomies proposed by researchers have contributed to this complexity, with some employing various terms for similar review characteristics, and others applying the same terms to studies with distinct review attributes. Consequently, a consensus regarding the categorisation of review studies, both in a broad context and specifically in mathematics education, remains elusive. We also observed instances of researchers labelling their reviews inaccurately. However, we refrained from judging the appropriateness of these terminologies as they fall outside the scope of our study and may be difficult to justify due to the ambiguity of the current typologies. Borges Migliavaca et al. (2020) expressed a similar concern, highlighting substantial disparities in review studies concerning their conceptualisation, conduct, reporting, risk of bias assessment, and data synthesis. They called for the evidence synthesis community to promptly develop guidance and reporting standards for review studies. Future researchers could potentially examine inconsistencies in the conducting of review studies and their categorisation in mathematics education. In this study, we distilled the various existing types of review studies to provide clear explanations of the main review types and to help researchers and readers understand the key characteristics of various review studies (see Chap. 2).
An additional noteworthy consideration pertains to the sample sizes of review studies. A prevalent discourse considers the appropriate number of studies to be included in a review, but establishing such a minimum or maximum number may be challenging and not appropriate because this depends on various contextual factors, such as the research area, topic, inclusion/exclusion criteria, and applied protocols. For example, in technical terms, a systematic review can be conducted with as few as two studies or as many as a thousand. A review study with a small sample (e.g. two or three studies) may be due to the literature search methods used or insufficient number of existing studies in a particular field, suggesting a limited demand for such a review. As previously noted, the primary function of review studies is to inform readers in the relevant field about published studies to address the challenge posed by an increasing number of studies and to identify trends and research gaps (Fusar-Poli & Radua, 2018). Conversely, although it is technically feasible to include a substantial number of studies in a review (e.g. 1,000 or 2,000), conducting a comprehensive analysis (e.g. content analysis) of such a large dataset can present major time, cost, storage, memory, bias, and security challenges (Cohen et al., 2015). Nevertheless, the findings of our study provide insight into this issue. Notably, the sample size of the studies we analysed varied from 8 to 3,485, with an average of 99. Notably, most of these studies (78%) had sample sizes of less than 100, with an average of 34. Although this observation does not serve as a prescriptive recommendation, it offers valuable insights into the typical sample sizes with which mathematics education researchers have tended to work in the past.
Furthermore, as evidenced by our findings, literature reviews may serve various purposes, such as assessing the use of theoretical models or conceptual and methodological approaches, or advancing new theories, concepts, or research models through critical appraisal of previous research within a specific subject area (Cooper, 1988). However, our findings also indicate that it is not common in practice to use or develop a theoretical or conceptual framework in mathematics education review studies. Only 24% of the reviewed studies explicitly reported employing a specific framework, and very few sought to formulate a framework based on the literature under scrutiny. The results highlighted the researchers’ interest in frameworks related to technology, knowledge, and competence models. A few studies incorporated grand theories, such as constructivism, sociocultural theory, and cognitive development theory.
It is remarkable that despite focusing on mathematics education, there is a notable scarcity of review studies employing content-specific frameworks in mathematics education, such as those centred on problem-solving, reasoning, and mathematical thinking. Only a minority of the studies used frameworks related to mathematical modelling and mathematical content knowledge. This observation may reflect a gap in the literature, suggesting a need for greater integration of domain-specific frameworks into review studies in mathematics education to enhance the depth and specificity of the studies. Moreover, this trend prompts a critical examination of potential underlying factors. One plausible explanation lies in the interdisciplinary nature of review studies in mathematics education, which draws contributions from diverse fields including psychology, educational technology, special education, and neuroscience. The diverse disciplinary backgrounds of the researchers may influence their preferences for frameworks that are not necessarily specific to mathematics education but rather draw from broader fields.
The bibliometric analysis revealed contributions to mathematics education, with 761 authors from 50 countries conducting review studies. In future studies, researchers may consider conducting detailed analyses of how these initiatives have influenced the landscape of mathematics education, examining their specific impacts on various subfields, and assessing their overall influence.
Our findings reveal a notable participation in literature review studies within mathematics education by scholars from diverse backgrounds, including educational psychologists, mathematics educators, and specialists in special education and neuroscience. This multidisciplinary engagement underscores the broader interest of researchers beyond the field of mathematics education. Notably, co-authorship connections within US institutions were the most extensive. The leading countries that published review studies included the US, Germany, China, Australia, and England. A robust network emerged among researchers in North America, Europe, Asia, and Australia, emphasising collaboration opportunities that warrant exploration by African and South American researchers.
Systematic reviews and meta-analyses stood out as the predominant review types in mathematics education, both in terms of the number of publications and citation counts. Systematic reviews offer rigorous and comprehensive syntheses of existing literature on specific research questions, providing valuable insights, identifying gaps in knowledge, and informing evidence-based decision-making in various fields. Moreover, meta-analyses enhance statistical power, resolve conflicting findings, and offer more precise estimates of effect sizes by combining data from various sources. However, there is a discernible need to diversify the types of reviews conducted in mathematics education.
The findings underscore a significant surge in both the quantity of review studies and their citation counts within mathematics education especially over the recent five-year period (2019–2023). This trend suggests a prevalent practice among authors to draw upon previously published reviews to contextualize their own studies, frequently engaging in discussions and citing references to corroborate or challenge existing findings. Such reliance on established literature highlights the discipline’s emphasis on leveraging prior knowledge to inform and substantiate new research endeavours.
The most cited review papers were associated with specific educational review journals, educational psychology journals, special education journals, educational technology journals, and mathematics education journals, further highlighting the interdisciplinary nature of impactful research in the field. The results revealed that ZDM– Mathematics Education, Educational Studies in Mathematics, International Journal of Science and Mathematics Education, and International Journal of Mathematical Education in Science and Technology were the key mathematics education journals committed to publishing review studies. The performance of these journals, particularly in recent years, reflects the escalating significance of review studies in mathematics education. Nevertheless, the limited visibility of some mathematics education journals in publishing review studies could be attributed, among other factors, to their restricted representation in the WoS database or to the overall small number of studies published yearly in particular mathematics education journals.
Prominent research topics in mathematics education review studies are digital technologies, technology-enhanced approaches (e.g. flipped classrooms), teacher education, mathematics achievement, early childhood education, and learning disabilities. Recent technological advances, including artificial intelligence and augmented/virtual reality, may soon attract mathematics education researchers’ attention to emerging technologies (Cevikbas, Bulut et al., 2023; Cevikbas, Greefrath et al., 2023). In addition to technology-enhanced mathematics education and special education, researchers have also explored the cognitive and affective aspects of learning and teaching mathematics.
In short, the absence of high-quality research syntheses may impede theoretical and conceptual advances within mathematics education (Webster & Watson, 2002). Therefore, future researchers may endeavour to develop discipline-specific standards and guidelines for conducting various types of review studies in mathematics education. Moreover, they could focus on expanding the content of mathematics education journals to accommodate a greater number of review studies. The scientific influence of review journals may also provide an opportunity to establish a dedicated review journal with a pronounced focus on mathematics education.
Finally, we want to point out that in this comprehensive meta-review, enriched by bibliometric analysis, we meticulously compiled and scrutinised the largest dataset of reviews in mathematics education available within the WoS database. Although this was a substantial sample (n = 259) that was reasonably representative of published review studies in mathematics education, it is important to acknowledge certain limitations. Our search was confined to WoS, and we specifically focused on review articles published in English. It is worth noting that the characteristics of review studies published in journals, international handbooks, or conference proceedings not indexed in WoS or published in a language other than English could potentially differ from those we examined. In addition, despite studies indexed in WoS theoretically being of high quality, we identified inconsistencies and variability in the review studies we examined, and it is possible that a more extensive search would have yielded different results.
In conclusion, we advocate producing high-quality review papers that adeptly synthesise available knowledge to improve professional practice (Templier & Paré, 2015). Such efforts may further advance mathematics education and contribute to the continuous improvement of teaching and learning activities, despite the demanding nature of comprehensive review studies.
Open Access funding enabled and organized by Projekt DEAL.